如何统计一个数字的二进制值里面有多少个1

发表于 更新于 分类于 阅读次数： 本文字数： 516 阅读时长 ≈ 2 分钟

任意给出一个正整数，例如4523，如何快速统计它的二进制值里面有几个1？

我们知道，在 Python 里面，查看一个数字的二进制函数为：bin，例如：

1
2
>>> bin(4523)
'0b1000110101011'

所以我们很快就能想到一个统计方案：

1
2
3
4
5
one_num = 0
for i in bin(4523)[2:]:
    if i == '1':
        count += 1
print(f'数字4523的二进制值里面，一共有{count}个1')

运行效果如下图所示：

如果使用这个方法，由于4523的二进制值有13位，所以 for 循环需要执行13次才能完成统计。更一般的结论，一个正整数 n，它的二进制值有$log_2{n} + 1$位，所以这种解法的时间复杂度始终为O(logn)，那么我们有没有什么办法优化这个算法呢？

这个时候，我们观察一个现象：

给出一个二进制的值1000110101011与这个值减1的值1000110101010，他们做与运算，结果为：1000110101010。可以看到，最右侧的1变成了0.

现在我们再对1000110101010与它减1的值做与运算：

1
1000110101010 & 1000110101001 = 1000110101000

此时，最右侧的1又变成了0.

我们可以证明，假设有一个二进制数 n与n-1做与运算，它的效果相当于把这个二进制数最右侧的1变成0.

于是，给定一个正整数x，只需要统计移除多少位的最右侧的1以后，这个数字变成了0，就能知道它里面有多少个1.于是我们可以写出如下的代码：

1
2
3
4
5
6
count = 0
n = 4523
while n:
    n = n & (n - 1)
    count += 1
print(count)

运行效果如下图所示：

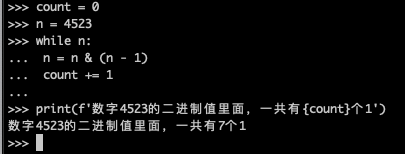
使用这种算法，最坏情况下，只有在数字 n 对应的二进制全部都是1的情况下(3, 7, 15, 31, 63….)，会执行$log_2n+1$次循环。而一般情况下，如果只有1个1，那么只需要循环1次，如果有2个1，只需要循环2次。大大提高了运算效率。